 +"""
+
+# ╔═╡ 3f56ec63-1fa6-403c-8d2a-1990382b97ae
+begin
+# === Your MILP model goes below ===
+# Replace the contents of this cell with your own model.
+sudoku = Model(HiGHS.Optimizer)
+
+# Variables should be a vector named x_s (used for testing)
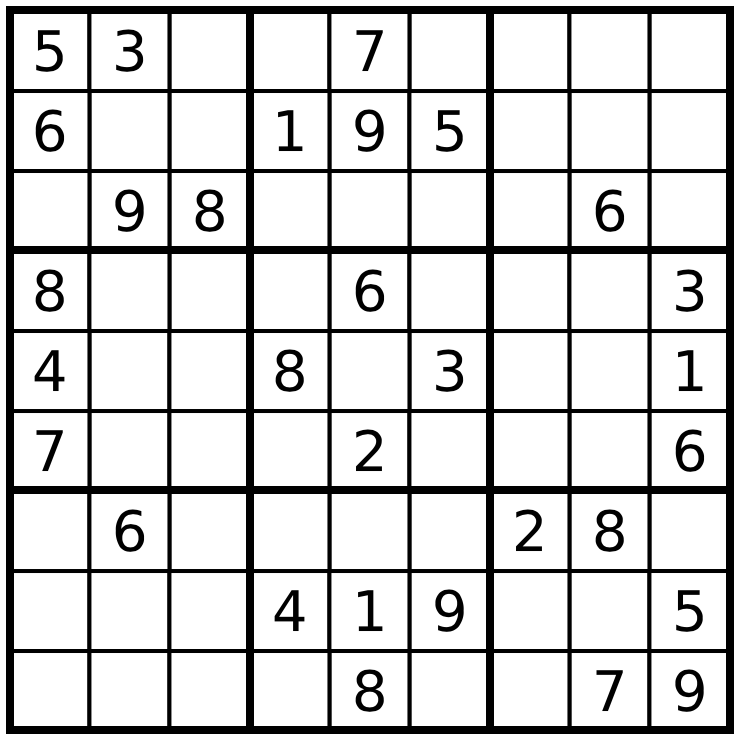
+@variable(sudoku, x_s[i = 1:9, j = 1:9, k = 1:9], Bin);
+
+# --- YOUR CODE HERE ---
+
+# optimize!(sudoku)
+
+# Let's look at the stats of our model
+sudoku
+end
+
+# ╔═╡ 0e8ed625-df85-4bd2-8b16-b475a72df566
+begin
+ ground_truth_s = (x_ss = [[ 5 3 4 6 7 8 9 1 2];
+ [6 7 2 1 9 5 3 4 8];
+ [1 9 8 3 4 2 5 6 7];
+ [8 5 9 7 6 1 4 2 3];
+ [4 2 6 8 5 3 7 9 1];
+ [7 1 3 9 2 4 8 5 6];
+ [9 6 1 5 3 7 2 8 4];
+ [2 8 7 4 1 9 6 3 5];
+ [3 4 5 2 8 6 1 7 9]])
+
+ anss = missing
+ try
+ anss = (
+ x_ss = haskey(sudoku, :x_s) ? JuMP.value.(sudoku[:x_s]) : missing,
+ )
+ catch
+ anss = missing
+ end
+
+ goods = !ismissing(anss) &&
+ all(isapprox.(anss.x_ss, ground_truth_s.x_ss; atol=1e-3))
+
+ if ismissing(anss)
+ still_missing()
+ elseif goods
+ correct()
+ else
+ keep_working()
+ end
end
+# ╔═╡ fa5785a1-7274-4524-9e54-895d46e83861
+md"""
+### 2.3 Other Modeling Tricks
+
+Below are some classic “tricks of the trade’’ for turning non-linear or logical
+requirements into **mixed-integer linear programming (MILP)** form.
+Throughout, $x\in\mathbb R^n$ are continuous decision variables and
+$z\in\{0,1\}$ are binary (0–1) variables.
+
+---
+
+#### Big-$M$ linearisation of conditional constraints
+Suppose a constraint should apply **only if** a binary variable is 1:
+
+```math
+z = 1 \;\Longrightarrow\; a^\top x \le b.
+```
+
+Introduce a sufficiently large constant $M>0$ and write
+
+```math
+a^\top x \;\le\; b + M\,(1-z).
+```
+
+* If $z=1$ the right-hand side is $b$, so the original constraint is enforced.
+* If $z=0$ the bound is relaxed by $M$ and becomes non-binding.
+
+> **Caveat:** pick $M$ as tight as possible. Over-large $M$ values hurt the LP
+> relaxation and may cause numerical instability.
+
+---
+
+#### Indicator constraints (a safer alternative)
+Modern solvers allow *indicator* constraints that internally handle the
+implication without an explicit $M$:
+
+```math
+z = 1 \;\Longrightarrow\; a^\top x \le b.
+```
+
+In JuMP:
+
+```julia
+@constraint(model, z --> a' * x <= b)
+```
+
+---
+
+"""
+
# ╔═╡ 5e3444d0-8333-4f51-9146-d3d9625fe2e9
md"""
---
-## 3. Non‑linear program – Rosenbrock valley
+## 3. Non‑linear program – Modified Rosenbrock valley
Non‑linear models dominate **optimal control** because discretising the differential equations that
describe a physical system almost always yields a **non‑linear program (NLP)**.
-A classic (and benign) test problem is the **Rosenbrock** function
+Let's modify the classic (and benign) **Rosenbrock** function
-\[
-\min_{x,\,y\in\mathbb R} \; f(x,y)= (1-x)^{2} + 100\,(y - x^{2})^{2}.
-\]
+```math
+\begin{aligned}
+\min_{x,\,y} \quad & f(x,y) \;=\; -(1-x)^{2} + 100\,(y - x^{2})^{2} + 10000x \\
+\text{s.t.}\quad & -10 \le x \le 10,\\
+ & -60 \le y \le 60.
+\end{aligned}
+```
-It has a single global optimum at \((x^{\star},y^{\star}) = (1,1)\) with \(f^{\star}=0\).
+It has a single global minimum within the feasible reagion defined by the box constraints on $x$ and $y$.
### 3.1 Your tasks
-1. Build and solve the model with **Ipopt**.
+1. Build a model to find this minimum and solve it with **Ipopt**.
2. Inspect the solution and objective.
-3. Check your work below.
+3. Pass the tests
"""
+# ╔═╡ 0e190de3-da60-41e9-9da5-5a0c7fefd1d7
+f(x, y) = -(1-x)^2 + 100 * (y-x^2)^2 + 10000*x
+
+# ╔═╡ cac18d70-b354-48c7-9f37-31ee0c585675
+begin
+# 1. Domain grids
+xs = range(-10, 10; length = 100) # 100 x-points
+ys = range(-60, 60; length = 100) # 100 y-points
+
+# 3. Surface heights — matrix z[y, x]
+zs = [f(x, y) for y in ys, x in xs]
+
+# 4. Create a 1×3 layout
+fig = Figure(size = (1500, 500))
+
+# 4a. 3-D surface
+ax3d = Axis3(fig[1, 1]; xlabel = "y", ylabel = "x", zlabel = "f(x,y)",
+ title = "Surface")
+surface!(ax3d, ys, xs, zs; colormap = :viridis)
+ax3d.azimuth[] = deg2rad(-10) # ≈ camera = (-10°, 30°)
+ax3d.elevation[] = deg2rad( 30)
+
+# 4b. Slice at y =
+y0=40
+ax_x = Axis(fig[1, 2]; xlabel = "x", ylabel = "f(x,$(y0))", title = "y = $(y0) slice")
+lines!(ax_x, xs, f.(xs, y0))
+
+# 4c. Slice at x =
+x_0 = 0
+ax_y = Axis(fig[1, 3]; xlabel = "y", ylabel = "f($(x_0),y)", title = "x = $(x_0) slice")
+lines!(ax_y, ys, f.(x_0, ys))
+
+fig
+end
+
# ╔═╡ 00728de8-3c36-48c7-8520-4c9f408a7c5f
begin
# === Your NLP model goes below ===
# Replace the contents of this cell with your own model.
model_nlp = Model(Ipopt.Optimizer)
+# Required named variables
+@variable(model_nlp, x)
+@variable(model_nlp, y)
+
# --- YOUR CODE HERE ---
# optimize!(model_nlp)
+
+println(model_nlp)
end
-# ╔═╡ 254b9a87-17f9-4fea-8b28-0e3873b58fe2
+# ╔═╡ 45541136-695a-4260-82c1-66d38ec44dcc
+md"""
+### 3.2 Intersecting-ellipse constraints
+Find the minimum of the same modified Rosenbrock objective, **but now the feasible
+region is the intersection of three ellipses** defined only through their focal points
+and the constant sum-of-distances $2a$:
+
+| Ellipse | Focal points $(p_1,\,p_2)$ | Required sum of distances $2a$ |
+|---------|---------------------------|--------------------------------|
+| $E_1$ | $(-4,\,0),\;(4,\,0)$ | $12$ |
+| $E_2$ | $(0,\,-5),\;(0,\,5)$ | $14$ |
+| $E_3$ | $(-3,\,-3),\;(3,\,3)$ | $12$ |
+
+Recall that a point $(x,y)$ lies **inside** an ellipse if the **sum of its Euclidean
+distances to the two foci is _no greater_ than $2a$**.
+Formulate these three nonlinear constraints and use **Ipopt** to locate the optimal
+$(x^*,y^*)$ and corresponding objective value.
+
+1. Implement the model with the three ellipse constraints.
+2. Solve it and report the optimal point and objective.
+3. Verify that the solver stopped at a feasible point (all three distance sums $\le 2a$).
+"""
+
+# ╔═╡ b107bcd7-60ca-4f09-aa42-f8335e13233e
begin
-# === Quick check ===
-@testset "NLP check" begin
- @test termination_status(model_nlp) == MOI.LOCALLY_SOLVED || termination_status(model_nlp) == MOI.OPTIMAL
- @test isapprox(objective_value(model_nlp), 0.0; atol = 1e-6)
-end
+ # ── NLP model ────────────────────────────────────────────────────────────────
+ model_nlp2 = Model(Ipopt.Optimizer)
+
+ # Decision variables with box bounds
+ @variable(model_nlp2, x2)
+ @variable(model_nlp2, y2)
+
+ # --- YOUR CODE HERE ---
+
+ # Solve
+ # optimize!(model_nlp2)
+
+ # Quick report
+ println(model_nlp2)
end
# ╔═╡ 147fe732-fe65-4226-af43-956b33a75bff
@@ -215,18 +654,160 @@ Getting comfortable with modelling and debugging small nonlinear examples like R
when you step up to thousands of variables in real control problems!
"""
+# ╔═╡ 87ffc247-3769-4002-a584-c687fd813125
+begin
+ hidden_answers = Dict(
+ :lp => (w = 20.0, g = 15.0, obj = 135.0),
+ :milp => (x = [1,1,1], obj = 22.0),
+ :nlp => (x = 1.0, y = 1.0, obj = 0.0),
+ )
+ safeval(model, sym) = haskey(model, sym) ? JuMP.value(model[sym]) : missing
+ md""
+end
+
+# ╔═╡ 6fb672d0-5a18-4ccc-b7b3-184839c2401b
+begin
+ # ground truth
+ ground_truth = (w = 20.0, g = 15.0, obj = 135.0)
+
+ # student answer
+ ans = missing
+ try
+ ans = (
+ w = safeval(model_lp, :w),
+ g = safeval(model_lp, :g),
+ obj = objective_value(model_lp),
+ )
+ catch # objective_value will throw if model_lp not ready
+ ans = missing
+ end
+
+ # Decide which badge to show
+ if ismissing(ans) # nothing yet
+ still_missing()
+ elseif isapprox(ans.w, ground_truth.w; atol=1e-3) &&
+ isapprox(ans.g, ground_truth.g; atol=1e-3) &&
+ isapprox(ans.obj, ground_truth.obj; atol=1e-3)
+ correct()
+ else
+ keep_working()
+ end
+end
+
+# ╔═╡ 20aef3e9-47b5-4f60-9726-7db77f7c3e47
+begin
+ # student answer
+ ansd = missing
+ try
+ ansd = safeval(model_lp2, :x_d)
+ catch # objective_value will throw if model_lp not ready
+ ansd = missing
+ end
+
+ # Decide which badge to show
+ if ismissing(ansd) # nothing yet
+ still_missing()
+ elseif x == 25.0
+ correct()
+ else
+ keep_working()
+ end
+end
+
+# ╔═╡ 254b9a87-17f9-4fea-8b28-0e3873b58fe2
+begin
+ ground_truth_3 = (x = -7.946795, y = 60.00, obj = -78554.7682)
+
+ ans3=missing
+ try
+ ans3 = (
+ x = safeval(model_nlp, :x),
+ y = safeval(model_nlp, :y),
+ obj = objective_value(model_nlp),
+ )
+ catch
+ ans3 = missing
+ end
+
+ good_2 = !ismissing(ans3) &&
+ isapprox(ans3.x, ground_truth_3.x; atol=1e-3) &&
+ isapprox(ans3.y, ground_truth_3.y; atol=1e-3) &&
+ isapprox(ans3.obj, ground_truth_3.obj; atol=1e-3)
+
+ if ismissing(ans3)
+ still_missing()
+ elseif good_2
+ correct()
+ else
+ keep_working()
+ end
+end
+
+# ╔═╡ 1fcaedb8-34d0-4faf-9052-fc074d2edda3
+begin
+ ground_truth_32 = (x = -3.121657, y = 2.875823, obj = -26515.3545)
+
+ ans4=missing
+ try
+ ans4 = (
+ x = safeval(model_nlp2, :x2),
+ y = safeval(model_nlp2, :y2),
+ obj = objective_value(model_nlp2),
+ )
+ catch
+ ans4 = missing
+ end
+
+ good_3 = !ismissing(ans4) &&
+ isapprox(ans4.x, ground_truth_32.x; atol=1e-3) &&
+ isapprox(ans4.y, ground_truth_32.y; atol=1e-3) &&
+ isapprox(ans4.obj, ground_truth_32.obj; atol=1e-3)
+
+ if ismissing(ans4)
+ still_missing()
+ elseif good_3
+ correct()
+ else
+ keep_working()
+ end
+end
+
# ╔═╡ Cell order:
# ╟─881eed45-e7f0-4785-bde8-530e378d7050
# ╟─9f5675a3-07df-4fb1-b683-4c5fd2a85002
+# ╟─b879c4bf-8292-45a0-87d0-b1f0fa456585
+# ╟─eeceb82e-abfb-4502-bcfb-6c9f76a0879d
# ╟─0df8b65a-0527-4545-bf11-00e9912bced0
# ╠═9ce52307-bc22-4f66-a4af-a4e4ac382212
# ╟─6f67ca7c-1391-4cb9-b692-cd818e037587
# ╠═49042d6c-cf78-46d3-bfee-a8fd7ddf3aa0
-# ╠═6fb672d0-5a18-4ccc-b7b3-184839c2401b
-# ╠═808c505d-e10d-42e3-9fb1-9c6f384b2c3c
+# ╟─1d3edbdd-7747-4651-b650-c6b9bf87b460
+# ╟─6fb672d0-5a18-4ccc-b7b3-184839c2401b
+# ╟─248b398a-0cf5-4c2b-8752-7b9cc4e765d6
+# ╟─245eb671-84e1-447b-8045-e9eb04966d80
+# ╟─6a823649-04fa-4322-a028-2fb29dffb08b
+# ╠═c369ab46-b416-4c12-83fe-65040a0c47c8
+# ╟─20aef3e9-47b5-4f60-9726-7db77f7c3e47
+# ╟─b13f9775-68c2-4646-9b67-c69ee23a4ea0
+# ╟─ea3ea95a-58cb-4d0d-a167-aa68b8bc2645
+# ╟─7d855c60-41dd-40af-b00a-60b3e779ad13
+# ╟─ae263aac-1668-4f18-8104-ac25953a4503
+# ╟─808c505d-e10d-42e3-9fb1-9c6f384b2c3c
# ╠═39617561-bbbf-4ef6-91e2-358dfe76581c
-# ╠═01367096-3971-4e79-ace2-83600672fbde
-# ╠═5e3444d0-8333-4f51-9146-d3d9625fe2e9
+# ╟─01367096-3971-4e79-ace2-83600672fbde
+# ╟─38b3a8f3-35ae-46da-91ce-0e4ba27ae098
+# ╟─bca712e4-3f1c-467e-9209-e535aed5ab0a
+# ╟─3997d993-0a31-435e-86cd-50242746c305
+# ╠═3f56ec63-1fa6-403c-8d2a-1990382b97ae
+# ╟─0e8ed625-df85-4bd2-8b16-b475a72df566
+# ╟─fa5785a1-7274-4524-9e54-895d46e83861
+# ╟─5e3444d0-8333-4f51-9146-d3d9625fe2e9
+# ╠═0e190de3-da60-41e9-9da5-5a0c7fefd1d7
+# ╟─cac18d70-b354-48c7-9f37-31ee0c585675
# ╠═00728de8-3c36-48c7-8520-4c9f408a7c5f
-# ╠═254b9a87-17f9-4fea-8b28-0e3873b58fe2
+# ╟─254b9a87-17f9-4fea-8b28-0e3873b58fe2
+# ╟─45541136-695a-4260-82c1-66d38ec44dcc
+# ╠═b107bcd7-60ca-4f09-aa42-f8335e13233e
+# ╟─1fcaedb8-34d0-4faf-9052-fc074d2edda3
# ╟─147fe732-fe65-4226-af43-956b33a75bff
+# ╟─87ffc247-3769-4002-a584-c687fd813125
diff --git a/class01/class01_intro.jl b/class01/class01_intro.jl
index 7e3f76f..781a102 100644
--- a/class01/class01_intro.jl
+++ b/class01/class01_intro.jl
@@ -49,6 +49,26 @@ md"
| Date | : | 28 of July, 2025 |
"
+# ╔═╡ ced1b968-3ba6-4e58-9bcd-bbc6bee2b93c
+md"#### Reference Material"
+
+# ╔═╡ 97994ed8-5606-46ef-bd30-c5343c1d99cf
+begin
+ MarkdownLiteral.@markdown(
+"""
+
+[^cmu]: Zachary Manchester et al. Optimal Control and Reinforcement Learning at Carnegie Mellon University - [CMU 16-745]("https://optimalcontrol.ri.cmu.edu/")
+
+[^OptProx]: Van Hentenryck, P., 2024. Fusing Artificial Intelligence and Optimization with Trustworthy Optimization Proxies. Collections, 57(02).
+
+[^ArmManip]: Guechi, E.H., Bouzoualegh, S., Zennir, Y. and Blažič, S., 2018. MPC control and LQ optimal control of a two-link robot arm: A comparative study. Machines, 6(3), p.37.
+
+[^ZachMIT]: Zachary Manchester talk at MIT - [MIT Robotics - Zac Manchester - Composable Optimization for Robotic Motion Planning and Control]("https://www.youtube.com/watch?v=eSleutHuc0w&ab_channel=MITRobotics").
+
+"""
+)
+end
+
# ╔═╡ 1f774f46-d57d-4668-8204-dc83d50d8c94
md"# Intro - Optimal Control and Learning
@@ -146,14 +166,200 @@ in stochastic programming.
# ╔═╡ 5d7a4408-21ff-41ec-b004-4b0a9f04bb4f
question_box(md"Can you name a few ways to try and/or solve this problem?")
+# ╔═╡ 7e487ebc-8327-4f3e-a8ca-1e07fb39991a
+md"""
+### Solution Methods
+
+There are a few ways to solve these problems:
+
+```math
+(\mathbf{x}_{t-1}, w_t)\xrightarrow[\pi_t^{*}(\mathbf{x}_{t-1}, w_t)]{
+\begin{align}
+ &\min_{\mathbf{x}_t, \mathbf{u}_t} \quad \! \! c(\mathbf{x}_t, \mathbf{u}_t) + \mathbf{E}_{t+1}[V_{t+1}(\mathbf{x}_t, w_{t+1})] \\
+ & \text{ s.t. } \quad\mathbf{x}_t = f(\mathbf{x}_{t-1}, w_t, \mathbf{u}_t) \nonumber \\
+ & \quad \quad \quad \! \! h(\mathbf{x}_t, \mathbf{u}_t) \geq 0. \nonumber
+\end{align}
+} (\mathbf{x}_t^{*}, \mathbf{u}_t^{*})
+```
+
+**Exact Methods:**
+ - Deterministic Equivalent: Explicitly model all decisions of all possible scenarios. (Good Luck!)
+ - Stochastic Dual Dynamic Programming, Progressive Hedging, ... (Hard but doable for some class of problems.)
+
+**Approximate Methods**:
+ - Approximate Dynamic Programming, (model-free and model-based)Reinforcement Learning, Two-Stage Decision Rules, ...
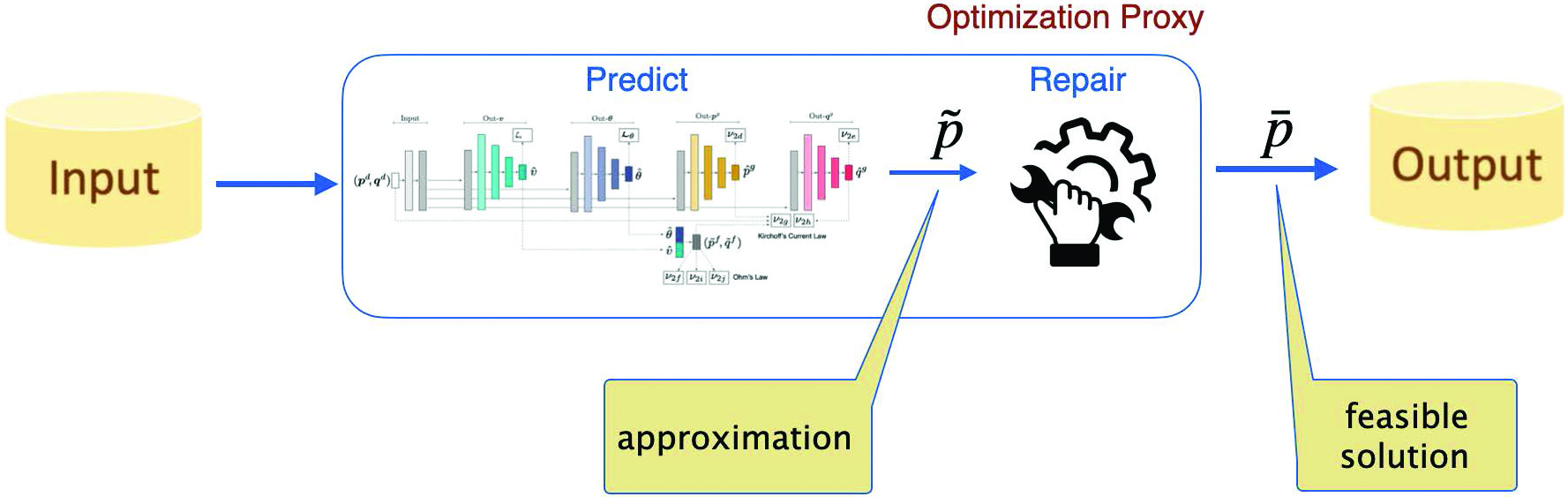
+ - **Optimization Proxies**:
+
+```math
+\theta^{\star}
+\;=\;
+\operatorname*{arg\,min}_{\theta \in \Theta}
+\;
+\mathbb{E}\Bigl[\bigl\|\,\pi_t^{\ast}-\pi_t(\,\cdot\,;\theta)\bigr\|_{\mathcal F}\Bigr],
+```
+
+"""
+
+# ╔═╡ bd623016-24ce-4c10-acb3-b2b80d4facc8
+md"[^OptProx]"
+
+# ╔═╡ 2d211386-675a-4223-b4ca-124edd375958
+@htl """
+
+
+"""
+
+# ╔═╡ 3f56ec63-1fa6-403c-8d2a-1990382b97ae
+begin
+# === Your MILP model goes below ===
+# Replace the contents of this cell with your own model.
+sudoku = Model(HiGHS.Optimizer)
+
+# Variables should be a vector named x_s (used for testing)
+@variable(sudoku, x_s[i = 1:9, j = 1:9, k = 1:9], Bin);
+
+# --- YOUR CODE HERE ---
+
+# optimize!(sudoku)
+
+# Let's look at the stats of our model
+sudoku
+end
+
+# ╔═╡ 0e8ed625-df85-4bd2-8b16-b475a72df566
+begin
+ ground_truth_s = (x_ss = [[ 5 3 4 6 7 8 9 1 2];
+ [6 7 2 1 9 5 3 4 8];
+ [1 9 8 3 4 2 5 6 7];
+ [8 5 9 7 6 1 4 2 3];
+ [4 2 6 8 5 3 7 9 1];
+ [7 1 3 9 2 4 8 5 6];
+ [9 6 1 5 3 7 2 8 4];
+ [2 8 7 4 1 9 6 3 5];
+ [3 4 5 2 8 6 1 7 9]])
+
+ anss = missing
+ try
+ anss = (
+ x_ss = haskey(sudoku, :x_s) ? JuMP.value.(sudoku[:x_s]) : missing,
+ )
+ catch
+ anss = missing
+ end
+
+ goods = !ismissing(anss) &&
+ all(isapprox.(anss.x_ss, ground_truth_s.x_ss; atol=1e-3))
+
+ if ismissing(anss)
+ still_missing()
+ elseif goods
+ correct()
+ else
+ keep_working()
+ end
end
+# ╔═╡ fa5785a1-7274-4524-9e54-895d46e83861
+md"""
+### 2.3 Other Modeling Tricks
+
+Below are some classic “tricks of the trade’’ for turning non-linear or logical
+requirements into **mixed-integer linear programming (MILP)** form.
+Throughout, $x\in\mathbb R^n$ are continuous decision variables and
+$z\in\{0,1\}$ are binary (0–1) variables.
+
+---
+
+#### Big-$M$ linearisation of conditional constraints
+Suppose a constraint should apply **only if** a binary variable is 1:
+
+```math
+z = 1 \;\Longrightarrow\; a^\top x \le b.
+```
+
+Introduce a sufficiently large constant $M>0$ and write
+
+```math
+a^\top x \;\le\; b + M\,(1-z).
+```
+
+* If $z=1$ the right-hand side is $b$, so the original constraint is enforced.
+* If $z=0$ the bound is relaxed by $M$ and becomes non-binding.
+
+> **Caveat:** pick $M$ as tight as possible. Over-large $M$ values hurt the LP
+> relaxation and may cause numerical instability.
+
+---
+
+#### Indicator constraints (a safer alternative)
+Modern solvers allow *indicator* constraints that internally handle the
+implication without an explicit $M$:
+
+```math
+z = 1 \;\Longrightarrow\; a^\top x \le b.
+```
+
+In JuMP:
+
+```julia
+@constraint(model, z --> a' * x <= b)
+```
+
+---
+
+"""
+
# ╔═╡ 5e3444d0-8333-4f51-9146-d3d9625fe2e9
md"""
---
-## 3. Non‑linear program – Rosenbrock valley
+## 3. Non‑linear program – Modified Rosenbrock valley
Non‑linear models dominate **optimal control** because discretising the differential equations that
describe a physical system almost always yields a **non‑linear program (NLP)**.
-A classic (and benign) test problem is the **Rosenbrock** function
+Let's modify the classic (and benign) **Rosenbrock** function
-\[
-\min_{x,\,y\in\mathbb R} \; f(x,y)= (1-x)^{2} + 100\,(y - x^{2})^{2}.
-\]
+```math
+\begin{aligned}
+\min_{x,\,y} \quad & f(x,y) \;=\; -(1-x)^{2} + 100\,(y - x^{2})^{2} + 10000x \\
+\text{s.t.}\quad & -10 \le x \le 10,\\
+ & -60 \le y \le 60.
+\end{aligned}
+```
-It has a single global optimum at \((x^{\star},y^{\star}) = (1,1)\) with \(f^{\star}=0\).
+It has a single global minimum within the feasible reagion defined by the box constraints on $x$ and $y$.
### 3.1 Your tasks
-1. Build and solve the model with **Ipopt**.
+1. Build a model to find this minimum and solve it with **Ipopt**.
2. Inspect the solution and objective.
-3. Check your work below.
+3. Pass the tests
"""
+# ╔═╡ 0e190de3-da60-41e9-9da5-5a0c7fefd1d7
+f(x, y) = -(1-x)^2 + 100 * (y-x^2)^2 + 10000*x
+
+# ╔═╡ cac18d70-b354-48c7-9f37-31ee0c585675
+begin
+# 1. Domain grids
+xs = range(-10, 10; length = 100) # 100 x-points
+ys = range(-60, 60; length = 100) # 100 y-points
+
+# 3. Surface heights — matrix z[y, x]
+zs = [f(x, y) for y in ys, x in xs]
+
+# 4. Create a 1×3 layout
+fig = Figure(size = (1500, 500))
+
+# 4a. 3-D surface
+ax3d = Axis3(fig[1, 1]; xlabel = "y", ylabel = "x", zlabel = "f(x,y)",
+ title = "Surface")
+surface!(ax3d, ys, xs, zs; colormap = :viridis)
+ax3d.azimuth[] = deg2rad(-10) # ≈ camera = (-10°, 30°)
+ax3d.elevation[] = deg2rad( 30)
+
+# 4b. Slice at y =
+y0=40
+ax_x = Axis(fig[1, 2]; xlabel = "x", ylabel = "f(x,$(y0))", title = "y = $(y0) slice")
+lines!(ax_x, xs, f.(xs, y0))
+
+# 4c. Slice at x =
+x_0 = 0
+ax_y = Axis(fig[1, 3]; xlabel = "y", ylabel = "f($(x_0),y)", title = "x = $(x_0) slice")
+lines!(ax_y, ys, f.(x_0, ys))
+
+fig
+end
+
# ╔═╡ 00728de8-3c36-48c7-8520-4c9f408a7c5f
begin
# === Your NLP model goes below ===
# Replace the contents of this cell with your own model.
model_nlp = Model(Ipopt.Optimizer)
+# Required named variables
+@variable(model_nlp, x)
+@variable(model_nlp, y)
+
# --- YOUR CODE HERE ---
# optimize!(model_nlp)
+
+println(model_nlp)
end
-# ╔═╡ 254b9a87-17f9-4fea-8b28-0e3873b58fe2
+# ╔═╡ 45541136-695a-4260-82c1-66d38ec44dcc
+md"""
+### 3.2 Intersecting-ellipse constraints
+Find the minimum of the same modified Rosenbrock objective, **but now the feasible
+region is the intersection of three ellipses** defined only through their focal points
+and the constant sum-of-distances $2a$:
+
+| Ellipse | Focal points $(p_1,\,p_2)$ | Required sum of distances $2a$ |
+|---------|---------------------------|--------------------------------|
+| $E_1$ | $(-4,\,0),\;(4,\,0)$ | $12$ |
+| $E_2$ | $(0,\,-5),\;(0,\,5)$ | $14$ |
+| $E_3$ | $(-3,\,-3),\;(3,\,3)$ | $12$ |
+
+Recall that a point $(x,y)$ lies **inside** an ellipse if the **sum of its Euclidean
+distances to the two foci is _no greater_ than $2a$**.
+Formulate these three nonlinear constraints and use **Ipopt** to locate the optimal
+$(x^*,y^*)$ and corresponding objective value.
+
+1. Implement the model with the three ellipse constraints.
+2. Solve it and report the optimal point and objective.
+3. Verify that the solver stopped at a feasible point (all three distance sums $\le 2a$).
+"""
+
+# ╔═╡ b107bcd7-60ca-4f09-aa42-f8335e13233e
begin
-# === Quick check ===
-@testset "NLP check" begin
- @test termination_status(model_nlp) == MOI.LOCALLY_SOLVED || termination_status(model_nlp) == MOI.OPTIMAL
- @test isapprox(objective_value(model_nlp), 0.0; atol = 1e-6)
-end
+ # ── NLP model ────────────────────────────────────────────────────────────────
+ model_nlp2 = Model(Ipopt.Optimizer)
+
+ # Decision variables with box bounds
+ @variable(model_nlp2, x2)
+ @variable(model_nlp2, y2)
+
+ # --- YOUR CODE HERE ---
+
+ # Solve
+ # optimize!(model_nlp2)
+
+ # Quick report
+ println(model_nlp2)
end
# ╔═╡ 147fe732-fe65-4226-af43-956b33a75bff
@@ -215,18 +654,160 @@ Getting comfortable with modelling and debugging small nonlinear examples like R
when you step up to thousands of variables in real control problems!
"""
+# ╔═╡ 87ffc247-3769-4002-a584-c687fd813125
+begin
+ hidden_answers = Dict(
+ :lp => (w = 20.0, g = 15.0, obj = 135.0),
+ :milp => (x = [1,1,1], obj = 22.0),
+ :nlp => (x = 1.0, y = 1.0, obj = 0.0),
+ )
+ safeval(model, sym) = haskey(model, sym) ? JuMP.value(model[sym]) : missing
+ md""
+end
+
+# ╔═╡ 6fb672d0-5a18-4ccc-b7b3-184839c2401b
+begin
+ # ground truth
+ ground_truth = (w = 20.0, g = 15.0, obj = 135.0)
+
+ # student answer
+ ans = missing
+ try
+ ans = (
+ w = safeval(model_lp, :w),
+ g = safeval(model_lp, :g),
+ obj = objective_value(model_lp),
+ )
+ catch # objective_value will throw if model_lp not ready
+ ans = missing
+ end
+
+ # Decide which badge to show
+ if ismissing(ans) # nothing yet
+ still_missing()
+ elseif isapprox(ans.w, ground_truth.w; atol=1e-3) &&
+ isapprox(ans.g, ground_truth.g; atol=1e-3) &&
+ isapprox(ans.obj, ground_truth.obj; atol=1e-3)
+ correct()
+ else
+ keep_working()
+ end
+end
+
+# ╔═╡ 20aef3e9-47b5-4f60-9726-7db77f7c3e47
+begin
+ # student answer
+ ansd = missing
+ try
+ ansd = safeval(model_lp2, :x_d)
+ catch # objective_value will throw if model_lp not ready
+ ansd = missing
+ end
+
+ # Decide which badge to show
+ if ismissing(ansd) # nothing yet
+ still_missing()
+ elseif x == 25.0
+ correct()
+ else
+ keep_working()
+ end
+end
+
+# ╔═╡ 254b9a87-17f9-4fea-8b28-0e3873b58fe2
+begin
+ ground_truth_3 = (x = -7.946795, y = 60.00, obj = -78554.7682)
+
+ ans3=missing
+ try
+ ans3 = (
+ x = safeval(model_nlp, :x),
+ y = safeval(model_nlp, :y),
+ obj = objective_value(model_nlp),
+ )
+ catch
+ ans3 = missing
+ end
+
+ good_2 = !ismissing(ans3) &&
+ isapprox(ans3.x, ground_truth_3.x; atol=1e-3) &&
+ isapprox(ans3.y, ground_truth_3.y; atol=1e-3) &&
+ isapprox(ans3.obj, ground_truth_3.obj; atol=1e-3)
+
+ if ismissing(ans3)
+ still_missing()
+ elseif good_2
+ correct()
+ else
+ keep_working()
+ end
+end
+
+# ╔═╡ 1fcaedb8-34d0-4faf-9052-fc074d2edda3
+begin
+ ground_truth_32 = (x = -3.121657, y = 2.875823, obj = -26515.3545)
+
+ ans4=missing
+ try
+ ans4 = (
+ x = safeval(model_nlp2, :x2),
+ y = safeval(model_nlp2, :y2),
+ obj = objective_value(model_nlp2),
+ )
+ catch
+ ans4 = missing
+ end
+
+ good_3 = !ismissing(ans4) &&
+ isapprox(ans4.x, ground_truth_32.x; atol=1e-3) &&
+ isapprox(ans4.y, ground_truth_32.y; atol=1e-3) &&
+ isapprox(ans4.obj, ground_truth_32.obj; atol=1e-3)
+
+ if ismissing(ans4)
+ still_missing()
+ elseif good_3
+ correct()
+ else
+ keep_working()
+ end
+end
+
# ╔═╡ Cell order:
# ╟─881eed45-e7f0-4785-bde8-530e378d7050
# ╟─9f5675a3-07df-4fb1-b683-4c5fd2a85002
+# ╟─b879c4bf-8292-45a0-87d0-b1f0fa456585
+# ╟─eeceb82e-abfb-4502-bcfb-6c9f76a0879d
# ╟─0df8b65a-0527-4545-bf11-00e9912bced0
# ╠═9ce52307-bc22-4f66-a4af-a4e4ac382212
# ╟─6f67ca7c-1391-4cb9-b692-cd818e037587
# ╠═49042d6c-cf78-46d3-bfee-a8fd7ddf3aa0
-# ╠═6fb672d0-5a18-4ccc-b7b3-184839c2401b
-# ╠═808c505d-e10d-42e3-9fb1-9c6f384b2c3c
+# ╟─1d3edbdd-7747-4651-b650-c6b9bf87b460
+# ╟─6fb672d0-5a18-4ccc-b7b3-184839c2401b
+# ╟─248b398a-0cf5-4c2b-8752-7b9cc4e765d6
+# ╟─245eb671-84e1-447b-8045-e9eb04966d80
+# ╟─6a823649-04fa-4322-a028-2fb29dffb08b
+# ╠═c369ab46-b416-4c12-83fe-65040a0c47c8
+# ╟─20aef3e9-47b5-4f60-9726-7db77f7c3e47
+# ╟─b13f9775-68c2-4646-9b67-c69ee23a4ea0
+# ╟─ea3ea95a-58cb-4d0d-a167-aa68b8bc2645
+# ╟─7d855c60-41dd-40af-b00a-60b3e779ad13
+# ╟─ae263aac-1668-4f18-8104-ac25953a4503
+# ╟─808c505d-e10d-42e3-9fb1-9c6f384b2c3c
# ╠═39617561-bbbf-4ef6-91e2-358dfe76581c
-# ╠═01367096-3971-4e79-ace2-83600672fbde
-# ╠═5e3444d0-8333-4f51-9146-d3d9625fe2e9
+# ╟─01367096-3971-4e79-ace2-83600672fbde
+# ╟─38b3a8f3-35ae-46da-91ce-0e4ba27ae098
+# ╟─bca712e4-3f1c-467e-9209-e535aed5ab0a
+# ╟─3997d993-0a31-435e-86cd-50242746c305
+# ╠═3f56ec63-1fa6-403c-8d2a-1990382b97ae
+# ╟─0e8ed625-df85-4bd2-8b16-b475a72df566
+# ╟─fa5785a1-7274-4524-9e54-895d46e83861
+# ╟─5e3444d0-8333-4f51-9146-d3d9625fe2e9
+# ╠═0e190de3-da60-41e9-9da5-5a0c7fefd1d7
+# ╟─cac18d70-b354-48c7-9f37-31ee0c585675
# ╠═00728de8-3c36-48c7-8520-4c9f408a7c5f
-# ╠═254b9a87-17f9-4fea-8b28-0e3873b58fe2
+# ╟─254b9a87-17f9-4fea-8b28-0e3873b58fe2
+# ╟─45541136-695a-4260-82c1-66d38ec44dcc
+# ╠═b107bcd7-60ca-4f09-aa42-f8335e13233e
+# ╟─1fcaedb8-34d0-4faf-9052-fc074d2edda3
# ╟─147fe732-fe65-4226-af43-956b33a75bff
+# ╟─87ffc247-3769-4002-a584-c687fd813125
diff --git a/class01/class01_intro.jl b/class01/class01_intro.jl
index 7e3f76f..781a102 100644
--- a/class01/class01_intro.jl
+++ b/class01/class01_intro.jl
@@ -49,6 +49,26 @@ md"
| Date | : | 28 of July, 2025 |
"
+# ╔═╡ ced1b968-3ba6-4e58-9bcd-bbc6bee2b93c
+md"#### Reference Material"
+
+# ╔═╡ 97994ed8-5606-46ef-bd30-c5343c1d99cf
+begin
+ MarkdownLiteral.@markdown(
+"""
+
+[^cmu]: Zachary Manchester et al. Optimal Control and Reinforcement Learning at Carnegie Mellon University - [CMU 16-745]("https://optimalcontrol.ri.cmu.edu/")
+
+[^OptProx]: Van Hentenryck, P., 2024. Fusing Artificial Intelligence and Optimization with Trustworthy Optimization Proxies. Collections, 57(02).
+
+[^ArmManip]: Guechi, E.H., Bouzoualegh, S., Zennir, Y. and Blažič, S., 2018. MPC control and LQ optimal control of a two-link robot arm: A comparative study. Machines, 6(3), p.37.
+
+[^ZachMIT]: Zachary Manchester talk at MIT - [MIT Robotics - Zac Manchester - Composable Optimization for Robotic Motion Planning and Control]("https://www.youtube.com/watch?v=eSleutHuc0w&ab_channel=MITRobotics").
+
+"""
+)
+end
+
# ╔═╡ 1f774f46-d57d-4668-8204-dc83d50d8c94
md"# Intro - Optimal Control and Learning
@@ -146,14 +166,200 @@ in stochastic programming.
# ╔═╡ 5d7a4408-21ff-41ec-b004-4b0a9f04bb4f
question_box(md"Can you name a few ways to try and/or solve this problem?")
+# ╔═╡ 7e487ebc-8327-4f3e-a8ca-1e07fb39991a
+md"""
+### Solution Methods
+
+There are a few ways to solve these problems:
+
+```math
+(\mathbf{x}_{t-1}, w_t)\xrightarrow[\pi_t^{*}(\mathbf{x}_{t-1}, w_t)]{
+\begin{align}
+ &\min_{\mathbf{x}_t, \mathbf{u}_t} \quad \! \! c(\mathbf{x}_t, \mathbf{u}_t) + \mathbf{E}_{t+1}[V_{t+1}(\mathbf{x}_t, w_{t+1})] \\
+ & \text{ s.t. } \quad\mathbf{x}_t = f(\mathbf{x}_{t-1}, w_t, \mathbf{u}_t) \nonumber \\
+ & \quad \quad \quad \! \! h(\mathbf{x}_t, \mathbf{u}_t) \geq 0. \nonumber
+\end{align}
+} (\mathbf{x}_t^{*}, \mathbf{u}_t^{*})
+```
+
+**Exact Methods:**
+ - Deterministic Equivalent: Explicitly model all decisions of all possible scenarios. (Good Luck!)
+ - Stochastic Dual Dynamic Programming, Progressive Hedging, ... (Hard but doable for some class of problems.)
+
+**Approximate Methods**:
+ - Approximate Dynamic Programming, (model-free and model-based)Reinforcement Learning, Two-Stage Decision Rules, ...
+ - **Optimization Proxies**:
+
+```math
+\theta^{\star}
+\;=\;
+\operatorname*{arg\,min}_{\theta \in \Theta}
+\;
+\mathbb{E}\Bigl[\bigl\|\,\pi_t^{\ast}-\pi_t(\,\cdot\,;\theta)\bigr\|_{\mathcal F}\Bigr],
+```
+
+"""
+
+# ╔═╡ bd623016-24ce-4c10-acb3-b2b80d4facc8
+md"[^OptProx]"
+
+# ╔═╡ 2d211386-675a-4223-b4ca-124edd375958
+@htl """
+
+ +
+"""
+
+# ╔═╡ 45275d44-e268-43cb-8156-feecd916a6da
+@htl """
+
+
+"""
+
+# ╔═╡ 45275d44-e268-43cb-8156-feecd916a6da
+@htl """
++ LearningToOptimize (L2O) is a collection of open-source tools + focused on the emerging paradigm of amortized optimization—using machine-learning + methods to accelerate traditional constrained-optimization solvers. + L2O is a work-in-progress; existing functionality is considered experimental and may + change. +
+ + +| + LearningToOptimize.jl + | ++ Flagship Julia package that wraps data generation, training loops and evaluation + utilities for fitting surrogate models to parametric optimization problems. + | +
| + DecisionRules.jl + | ++ Build decision rules for multistage stochastic programs, as proposed in + Efficiently + Training Deep-Learning Parametric Policies using Lagrangian Duality. + | +
| + L2OALM.jl + | ++ Implementation of the primal-dual learning method ALM, + introduced in + + Self-Supervised Primal-Dual Learning for Constrained Optimization. + | +
| + L2ODLL.jl + | ++ Implementation of the dual learning method DLL, + proposed in + + Dual Lagrangian Learning for Conic Optimization. + | +
| + L2ODC3.jl + | ++ Implementation of the primal learning method DC3, as described in + + DC3: A Learning Method for Optimization with Hard Constraints. + | +
| + BatchNLPKernels.jl + | ++ GPU kernels that evaluate objectives, Jacobians and Hessians for + batches of + ExaModels, + useful when defining loss functions for large-batch ML predictions. + | +
| + BatchConeKernels.jl + | ++ GPU kernels for batched cone operations (projections, distances, etc.), + enabling advanced architectures such as repair layers. + | +
| + LearningToControlClass + | ++ Course repository for Special Topics on Optimal Control & Learning + (Fall 2025, Georgia Tech). + | +
+ The + + LearningToOptimize 🤗 Hugging Face organization + hosts datasets and pre-trained weights that can be used with L2O packages. +
+ +