🔐 Digital VLSI Circuit Design, ASIC Chip Design and FPGA Prototyping of Post-Processing tasks for Quantum Key Distribution Systems
Classical post-processing simulation for Quantum Key Distribution (QKD) based on the BB84 protocol.
This project is implemented in C++ is used to simulate classical post-quantum steps, while hardware modules are implemented in Verilog.” and simulates the classical steps after quantum transmission:
This project focuses on Quantum Key Distribution (QKD), a method for secure key sharing immune to quantum attacks. The raw key from a QKD system contains errors and redundancy, requiring post-processing steps: Sifting, Error Estimation, Error Correction, and Privacy Amplification (PA).
The algorithms for Sifting and PA were first implemented and tested in C/C++, allowing rapid prototyping and functional simulation. After verifying correctness, the design was migrated to hardware using Verilog HDL and tested on Xilinx Vivado, achieving real-time performance with low latency.
This work demonstrates the transition from software simulation to digital VLSI implementation, providing an efficient and scalable solution for secure quantum communication.
Quantum Key Distribution (QKD) is a method for generating and securely sharing a cryptographic key between two parties, traditionally called Alice (sender) and Bob (receiver), using the principles of quantum mechanics.
Unlike classical key exchange protocols (e.g., RSA or Diffie-Hellman), QKD is theoretically unbreakable due to the no-cloning theorem and quantum uncertainty.
The most common protocol is BB84, where photons are encoded with quantum states (polarizations), and measurement outcomes depend on the chosen basis.
Example:
- Alice sends quantum bits (qubits) encoded in random bases.
- Bob measures these qubits in random bases.
- Only when their bases match do they keep the result, forming the sifted key.
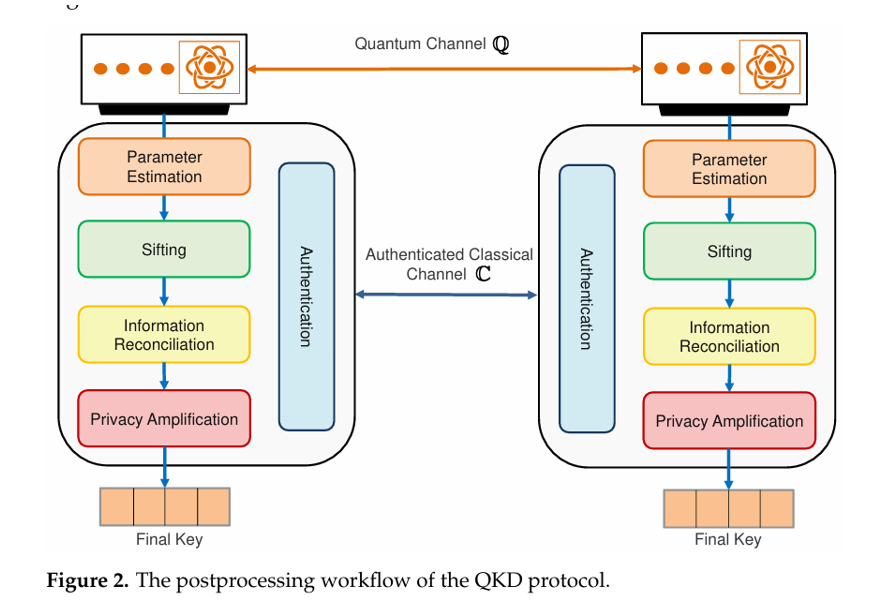
The standard post-processing pipeline in most QKD protocols consists of:
-
Sifting
Keep only the bits where Alice's and Bob's measurement bases match, forming the sifted key. -
Parameter Estimation / QBER Calculation
Estimate the Quantum Bit Error Rate (QBER) to assess the level of eavesdropping or channel noise. -
Error Correction (Information Reconciliation)
Correct errors in the sifted key due to channel noise or imperfections in photon transmission. -
Privacy Amplification (Toeplitz matrix)
Compress the corrected key using universal hashing techniques to produce a final secure key, removing any partial information an eavesdropper may have.
The following figure illustrates the post-processing steps in a typical QKD protocol, showing the flow from quantum transmission to the final secure key:
This project simulates the post-processing steps of Quantum Key Distribution (QKD) — focusing on error detection, correction, and privacy amplification — using the BB84 protocol principles.
The goal is to demonstrate how Alice and Bob can generate a shared secret key while ensuring it is free from errors and secure against eavesdropping.
- Programming Language: C++
- Platform: VS Code on Windows
- Compiler: g++
- Libraries: Standard C++ Libraries, Custom
qkdtools::PrivAmpclass
The simulation covers four main phases:
- Parameter Estimation
- Sifting
- Information Reconciliation (Error Detection)
- Privacy Amplification
Each phase ensures the security, integrity, and synchronization of the final shared key.
- The simulation successfully demonstrates how QKD post-processing works in practice.
- Even with errors introduced, privacy amplification ensures a secure final key.
- Error correction (e.g., LDPC codes) can be added for further synchronization.
- Implement LDPC-based error correction.
- Extend sifting to support basis comparison as in real BB84.
- Add network simulation between Alice and Bob.
- Integrate with FPGA hardware layer for real-world deployment.
main.cpp→ Controls simulation flowPrivAmp.h / PrivAmp.cpp→ Handles Toeplitz-based privacy amplification- Utility Functions → Bit printing, mismatch analysis, and QBER calculation
The complete source code for the C++ simulation is available here:
👉 QKD C++ Post-Processing Code
In a Quantum Key Distribution (QKD) system, sifting is the first and most fundamental post-processing step performed after quantum transmission of photons. Its goal is to keep only those bits where Alice and Bob used the same basis, forming the sifted key.
- In BB84, Alice and Bob randomly select measurement bases (+ or ×).
- Only when their bases match, the measured bit is meaningful.
- Mismatched basis measurements are discarded.
- Output: Shorter but more reliable key.
Example Table:
| Photon Index | Alice Basis | Bob Basis | Keep Bit? | Alice Bit | Bob Bit |
|---|---|---|---|---|---|
| 1 | + | + | ✅ Yes | 1 | 1 |
| 2 | + | × | ❌ No | 0 | 0 |
| 3 | × | × | ✅ Yes | 1 | 1 |
| 4 | × | + | ❌ No | 0 | 1 |
👉 Sifted Key = {1, 1}
To enable real-time high-throughput QKD, sifting is implemented in hardware (FPGA/ASIC).
Objectives of Hardware Block:
- Compare Alice & Bob’s bases.
- Store only matching bits in memory.
- Count matches until a target length (e.g., 10 bits).
- Compute QBER (errors in matched bits).
| Component | Function | Importance |
|---|---|---|
| LFSR8 | Random bit & basis generator | Simulates Alice’s randomness |
| MUX2to1 | Switch manual/random inputs | For flexible testing |
| Comparator | Basis equality check | Core sifting rule |
| FSM | Controls state flow | Manages compare → store → finish |
| Counter | Counts sifted bits | Generates memory addresses |
| DFF | Synchronizes signals | Reliable timing |
| reg_mem | Stores sifted key bits | Temporary secure storage |
- Simulation Output: Shows sifted key bits stored in memory.
- Waveform: Confirms FSM transitions, valid bit storage, and QBER computation.
The complete Verilog implementation of the Sifting Block is available here:
👉 Verilog HDL for QKD Sifting
In Quantum Key Distribution (QKD), even after error correction, the shared secret key might partially leak information to an eavesdropper (Eve).
Privacy Amplification (PA) is the final post-processing step, ensuring that the final key is shorter but information-theoretically secure.
Goal: Compress the corrected key so that even if Eve has partial knowledge, the final key appears completely random to her.
- Quantum noise & hardware imperfections may leak info.
- Eve could intercept & resend photons (causing QBER).
- Error correction leaks parity bits during reconciliation.
PA ensures:
- Removal of Eve’s knowledge
- Perfect secrecy of the final key
PA uses universal hash functions to compress the key.
🔹 Formula:
If
K= input key (length n)H(K)= entropy of the keyl= final key lengthε= security parameter
Then:
l ≤ H(K) − 2*log2(1/ε)
🔹 Methods Used:
- Toeplitz matrices
- Universal Hash Functions (MMH-MH)
- Number Theoretic Transform (NTT) for fast modular arithmetic
To achieve real-time performance, PA is implemented in FPGA/ASIC.
Main Components:
- Input Buffer (corrected key storage)
- Seed Generator (random seeds for hash)
- Universal Hash Core (NTT-based polynomial multiplication)
- Compression Logic (shortens key based on QBER)
- Output Register (final secure key)
-
Barrett or Montgomery modular reduction
-
Parallel butterfly units in NTT
-
Bit-slicing & pipelining for speed

The Number Theoretic Transform (NTT) is analogous to FFT but over finite fields.
Steps for multiplying polynomials A(x), B(x):
- Forward NTT on A(x), B(x)
- Pointwise multiplication
- Inverse NTT → C(x)
You implemented a 2×2 NTT Butterfly Module:
- Inputs:
fi_0,fi_1(24-bit each) - Twiddle-factor multiplication with modular reduction
- Outputs:
Fi_0,Fi_1
Modules:
mult_gen_0→ modular multipliersc_add_0→ addersbarret.v→ efficient modulo-q reduction
Parameters:
- Modulus:
q = 8380417 - Root of unity:
r = 1753
Butterfly Equations: Fi_0 = fi_0 + (r^α mod q) * fi_1 Fi_1 = fi_0 + (−r^α mod q) * fi_1
- ntt_butterfly_2x2.v → Top module for NTT butterfly
- barret.v → Barrett reduction logic
- dummy_modules.v → Placeholder IPs for simulation
- tb_ntt_butterfly_2x2.v → Testbench
Testbench Output Example: Time fi_0 fi_1 => Fi_0 Fi_1 150000 5 3 => 14424587 10716674 250000 9 6 => 12071957 4656131
| Module | Purpose |
|---|---|
| ntt_butterfly_2x2.v | Core butterfly (NTT) operation |
| barret.v | Efficient modular reduction |
| dummy_modules.v | Placeholders for IP blocks |
| tb_ntt_butterfly_2x2.v | Simulation & verification |
✅ Verified using Vivado 2018.2
✅ Outputs matched expected values
✅ RTL confirmed correct modular arithmetic
RTL Schematic:
Output:
Waveform:
-
Language: Verilog HDL
-
Simulation Tool: Xilinx Vivado Simulator (2018.2)
-
Bit Width: 24-bit modular arithmetic
-
Modules Created:
ntt_butterfly_2x2.v(2×2 NTT butterfly core)barret.v(modular reduction)tb_ntt_butterfly_2x2.v(testbench)
-
Design Verified For: 3 test vector sets
-
Cycle Count: One butterfly operation completes in a few clock cycles
-
Target Hardware: FPGA/ASIC for real-time QKD post-processing
| Component | Description |
|---|---|
| Input FIFO | Stores corrected key bits |
| NTT Core | Fast modular multiplication |
| Universal Hash Gen | Implements MMH-MH family |
| Barrett Reducer | Reduces mod q |
| Output Register | Stores final secret key |
| FSM Controller | Manages timing & QBER-based logic |
In this project, two crucial post-processing blocks of Quantum Key Distribution (QKD) — Sifting and Privacy Amplification (PA) — were successfully designed and implemented using Verilog HDL and simulated in Xilinx Vivado.
-
Sifting Block: Responsible for comparing quantum bases and filtering out invalid key bits. It ensured that only the matched basis bits were retained, which is essential for secure key generation and minimizing the Quantum Bit Error Rate (QBER).
-
Privacy Amplification Block: Implemented using a hardware-optimized 2×2 NTT (Number Theoretic Transform) butterfly architecture. This module compressed the sifted key and eliminated any remaining partial knowledge an eavesdropper might possess. The use of NTT enabled efficient and secure hashing through modular polynomial multiplication.
Simulation results validated the correct functionality and timing of both blocks. The outputs matched expected values, confirming the reliability of the architecture.
This work demonstrates a foundational step toward hardware acceleration of QKD post-processing, contributing to the development of real-time quantum-secure communication systems.
Results:
- Both blocks successfully simulated in Vivado
- Verified correctness with multiple test vectors
- Provides real-time hardware acceleration for QKD post-processing
👉 Full Verilog source code is available here:
🔗 Verilog HDL for QKD Privacy Amplification
Quantum Key Distribution has direct applications in securing highly sensitive data across various domains:
- Government Communications: Protecting national security information and diplomatic communications.
- Financial Transactions: Securing banking, stock exchanges, and other high-value data transfers.
- Healthcare: Ensuring the privacy and integrity of sensitive patient records.
- Critical Infrastructure: Safeguarding energy grids, water systems, and transportation networks from cyberattacks.
- Educational demonstrations of QKD post-processing
- Hardware acceleration of QKD for FPGA/ASICs
- Research prototype for real-time quantum-secure communication systems
- An FPGA-Based 4 Mbps Secret Key Distillation Engine for Quantum Key Distribution Systems
- Software Bundle for Data Post-Processing in a Quantum Key Distribution Experiment
- An Overview of Postprocessing in Quantum Key Distribution
- Large-scale and High-speed Privacy Amplification for FPGA-based Quantum Key Distribution
- High-speed Implementation of Privacy Amplification in Continuous Variable Quantum Key Distribution
- A Real-Time QKD System Based on FPGA
- A Complete Beginner Guide to the Number Theoretic Transform (NTT) – Ardianto Satriawan, Rella Mareta, Hanho Lee
- Open-Source FPGA Implementation of Number-Theoretic Transform for CRYSTALS-Dilithium
- Quantum Cryptography and Secret-Key Distillation
- Protecting Information: From Classical Error Correction to Quantum Cryptography