Density & Score Lab: Interactive AI Visualizer

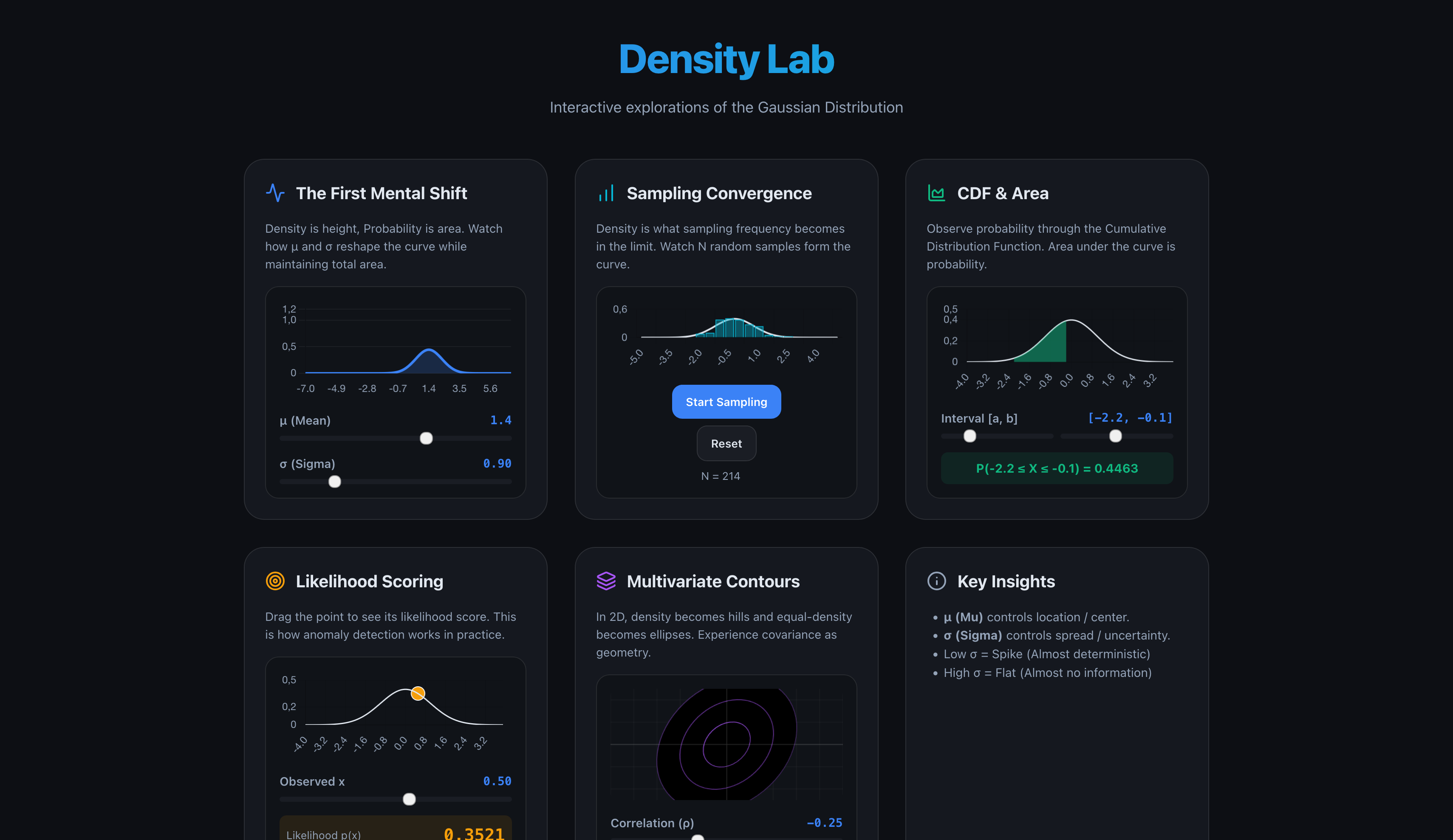
A premium, interactive web application designed to build a deep intuition for continuous probability distributions, the Score function, and the foundations of Diffusion Models.

🧭 Navigation

The lab is organized into three specialized tabs:

1. Foundations: Core Gaussian properties, sampling convergence, and CDF calculus.
2. Score Theory: The mathematics of $\nabla \log p(x)$, ISM vs ESM, and Pseudo-Likelihood.
3. Diffusion Labs: Forward SDE processes and Denoising Score Matching (DSM).

🌟 Features

1. The First Mental Shift

• Intuition: Density ≠ Probability.
• Interactive: Sliders for $\mu$ (mean) and $\sigma$ (standard deviation) show how the "height" (density) changes while the "area" (probability) remains 1.

2. Sampling Convergence

• Intuition: Density is what sampling frequency becomes in the limit.
• Interactive: Generate random samples in real-time and watch the histogram converge to the theoretical PDF ($p(x)$).

3. CDF & Area Highlighting

• Intuition: $P(a \leq X \leq b) = \int_{a}^{b} p(x) dx$.
• Interactive: Drag interval boundaries and see the shaded area calculate the cumulative probability.

4. Likelihood Scoring

• Intuition: Density as a "Normality Score".
• Interactive: Drag a point along the axis to see its likelihood. Highlights how anomaly detection is mathematically grounded in density values.

5. Multivariate Gaussian (2D)

• Intuition: Covariance is Geometry.
• Interactive: Adjust correlation ($\rho$) and observe how the density "hills" tilt and stretch into ellipses.

6. Score Function & Matching

• Intuition: $s(x) = \nabla \log p(x)$ points to the peak.
• Interactive: Watch the "score field" (vector arrows) pull points toward the data mode. Essential for understanding Diffusion Models and Energy-Based Models.

7. Pseudo-Likelihood (Besag, 1974)

• Intuition: Maximize individual conditional likelihoods $p(x_i | x_{-i})$ instead of the full joint.
• Interactive: Observe conditional Gaussian slices and watch the product reach its max at the true parameter value. Efficient for models with intractable normalizers.

8. Forward Diffusion

• Intuition: Structured patterns dissolve into Gaussian noise.
• Interactive: Corrupt a "data manifold" with increasing $\sigma$ levels to visualize the forward process used in SDE and Diffusion models.

9. ISM vs ESM Identity (Hyvärinen, 2005)

• Intuition: $J_{ESM}(\theta) = J_{ISM}(\theta) + C$.
• Interactive: Minimize the Implicit Score Matching objective without ever knowing the ground-truth density. Watch how matching the "divergence" of the score field is equivalent to matching the vectors.

10. Denoising Score Matching (Vincent, 2011)

• Intuition: Score Matching is equivalent to Denoising Autoencoders (SMDAE).
• Interactive: Perturb a clean sample $x$ with noise to get $\tilde{x}$. The DSM objective trains the model to point from $\tilde{x}$ back to $x$, which is equivalent to estimating the score of the data distribution.

11. 2D Point Cloud Diffusion (Ho et al., 2020)

• Intuition: The "Hello World" of generative models. Watch the full diffusion process in action.
• Interactive: Generate 2D point clouds (circle, spiral, multi-modal, moon) and watch them evolve from pure Gaussian noise to structured shapes. Real-time formula evaluation shows $\sqrt{\bar{\alpha}_t}$ values during animation.

🚀 Tech Stack

• Framework: React (Vite)
• Styling: Vanilla CSS (Modern design system, Dark Mode, Glassmorphism)
• Plotting: Chart.js + react-chartjs-2
• Math Rendering: KaTeX for real-time LaTeX evaluation.
• Math Logic: Box-Muller transform for sampling, Error Function approximations for CDF.

🛠️ Getting Started

# Clone the repository
git clone https://github.com/VicoErv/density-lab.git

# Install dependencies
npm install

# Start development server
npm run dev

# Build for production
npm run build

� References

This project implements and visualizes concepts from the following foundational papers:

• Hyvärinen, A. (2005). Estimation of Non-Normalized Statistical Models by Score Matching. Journal of Machine Learning Research, 6(24), 695-709.

  • Introduced Score Matching and the ISM/ESM equivalence for learning unnormalized models.

• Vincent, P. (2011). A Connection Between Score Matching and Denoising Autoencoders. Neural Computation, 23(7), 1661-1674.

  • Proved that Denoising Autoencoders (DAE) are equivalent to Score Matching under Gaussian noise.

• Ho, J., Jain, A., & Abbeel, P. (2020). Denoising Diffusion Probabilistic Models. NeurIPS 2020.

  • Foundational paper on DDPM, establishing connections between diffusion models and denoising score matching with Langevin dynamics.

• Besag, J. (1974). Spatial Interaction and the Statistical Analysis of Lattice Systems. Journal of the Royal Statistical Society: Series B, 36(2), 192-225.

  • Introduced Pseudo-Likelihood for models with intractable partition functions.

�📜 License

MIT