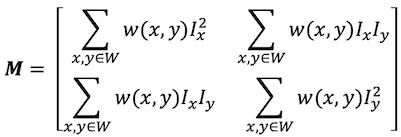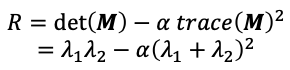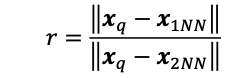Machine Vision System

Mount Google Drive

from google.colab import drive
drive.mount('/content/gdrive')

Make a new folder

import os
path='/content/gdrive/MyDrive/폴더명'
os.mkdir(path)

---

Camera calibration

• code
  
• image

Calibration (camera matrix, distortion coefficients, rotation and translation vectors)

ret, mtx, dist, rvecs, tvecs = cv.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)

가로 길이 1, 세로 길이 3, 높이 5 인 직육면체를 checkerboard (0,0,0)을 기준

axis = np.float32([[0,0,0], [0,5,0], [1,5,0], [1,0,0], [0,0,-3], [0,5,-3], [1,5,-3], [1,0,-3]])

가로 길이 1, 세로 길이 3, 높이 5 인 직육면체를 checkerboard (2,2,0)을 기준

axis = np.float32([[2,2,2], [2,7,2], [3,7,2], [3,2,2], [2,2,-1], [2,7,-1], [3,7,-1], [3,2,-1]])

---

Average filter

• code
• image

Kernel의 크기 변경하며 수행

blur = cv.blur(img, ksize=( , ))

---

Image sharpening

• code
• image

𝛼를 변경하며 수행

shapened_img = np.int32(img) + 𝛼 * detail 

---

Gasussian filter

• [code]
• image
• getGaussianKernel
• filter2D

kerner1d의 outer product를 계산하여 kernel2d 생성

kernel2d = np.outer(kernel1d, kernel1d.transpose())

---

Salt and pepper noise & Median filtering

• code
• image

---

Sobel filter

• code

---

RANSAC line fitting

• A simple but Clever Idea

  • What we really want: model explains many points "well"
  • Least Squares: model makes as few big mistakes as possible over the entire dataset
  • New objective: find model for which error is "small" for as many data points as possible
  • Method: RANSAC (RAndom SAmple Consensus)

• RANSAC: Pros and Cons
  

  	Pros	Cons
  1	Ridiculously simple	Have to tune parameters
  2	Ridiculously effective	No theory (so can not derive parameters via theory)
  3	Works in general	Not magic, especially with lots of outliers

• draw line (cv.line)

---

Harris Corner Detector

1. Compute partial derivatives lx, ly per pixel
2. Compute M at each pixel, using Gaussian weighting w
3. Compute response function R
4. Threshold R
5. Take only local maxima (Non-Maxima Suppression, NMS)

• code
• image
• image rotation (cv.rotate)

---

SIFT (based Blob Detector)

(* SIFT: Scale Invariant Feature Transform)

• Blob Detection : Find maxima and minima of blob filter response in scale and space
  • With Laplacian
    • Edge : zero-crossing
    • Blob : Two edges in opposite directions
    • When blob is just the rught size, Laplacian gives a large absolute value
  • In scale space
    • Convolve image with Laplacian at several scales
    • Find local maxima and minima of squared Laplacian response in image+sclae space
• code
• image

---

SIFT (based Local Descriptors)

• SIFT
  • Descriptors
    1. Normalize the rotation/scale of the patch
    2. Compute gradient at each pixel
    3. Divide into sub-patch (here 2x2, actually 4x4)
    4. In each sub-patch, compute histogram of 8 gradient directions
    5. Describe the patch with 4x4x8=128 numbers
  • Properties
    • Using graidients gives invariance to illumination
    • Using histogram of patches gives invariance to small/rotations
    • Compactly describe local appearance of patches with 128-dim vector
    • It can handle up to ~60 degrees out-of-plane rotation & chages of illumination
    • Fast and efficient and lots of code available
  • Features: Instance Matching
    • Given a features xq, instaed of finding the nearest neighbor to xq, find the nearest neighbor and second nearest neighbor
    • This ratio is a good test for matches:

• code
• image

---

Homograhy estimation

• [code]
• [image]